Dr. J's Maths.com
Where the techniques of Maths
are explained in simple terms.

Calculus - Differentiation - drawing derivative curves.
Test Yourself 1 - Solutions.


 

Questions on this page require drawing derivative graphs:
1. Given equations of any of the main types of functions.
2. Given graphs of functions.

 

From given equations.

Draw the graph for each of the given functions in Q 1 - 21.
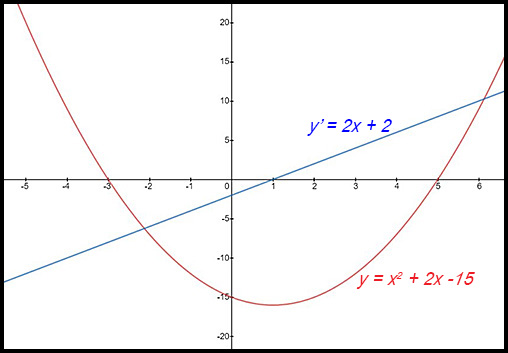
Then draw the graph of the derivative function either on the same set of axes or underneath depending on which presentation you consider shows your graph clearer.
If you choose to draw separate axes underneath, ensure the y axes are aligned.
Given a parabola. 1. y = (x + 3)(x - 5)

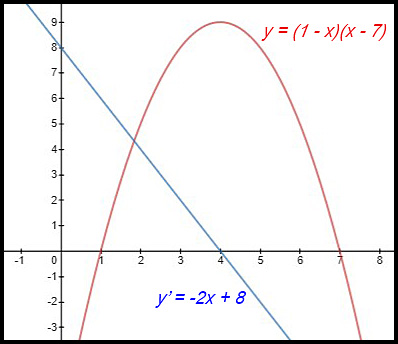
  2. y = (1 - x)(x - 7)

At x = 4, the derivative curve has a value of 0
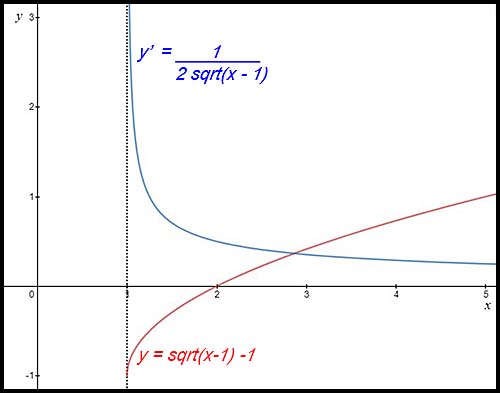
while the original curve has a maximum value of 9.
Hence the tangent to the original curve at x = 4 is horizontal.
  3. (i)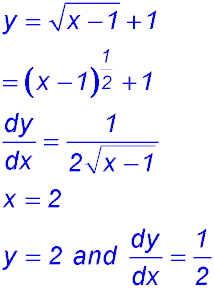

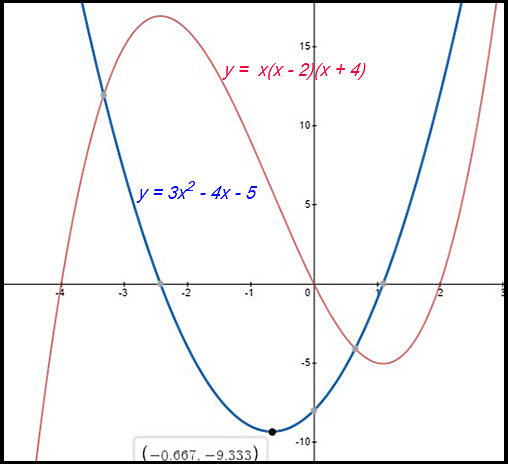
(ii)

The derivative graph is always above the x axis because the gradient of the original function is always positive.

As the value of x increases, the gradient decreases and so the graph approaches the x axis.

Given a cubic 4. y = x(x - 2)(x + 4) = x3 + 2x2 - 8x

y' = 3x2 + 4x - 8

At about x = -0.7 (say -0.667), the derivative curve has
a minimum value (of about = -9.3). Hence the gradient of the original curve is steepest - in a negative direction.

The original curve at that point has a y value (ordinate)
of nearly 6.

When the derivative curve has a minimum or maximum value
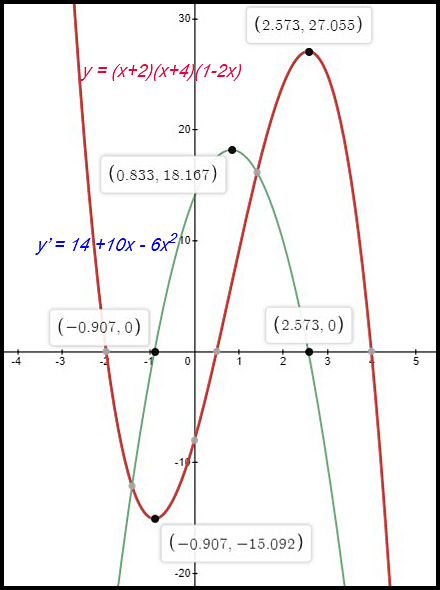
(i.e. a gradient of zero), there is a point of inflection
in the original curve.
  5. y = (x + 2)(1 - 2x)(x - 4)

(iii) When x = -0.907, the derivative curve has y = 0
and the original curve has y = -15.092.
Hence there is a stationary point at (-0.903, -15.092).

When x = 2.573, the derivative curve has y = 0
and the original curve has y = 27.055.
Hence there is a stationary point at (2.573, 27.055).

When x = 0.833, the derivative curve has y' = 18.167.
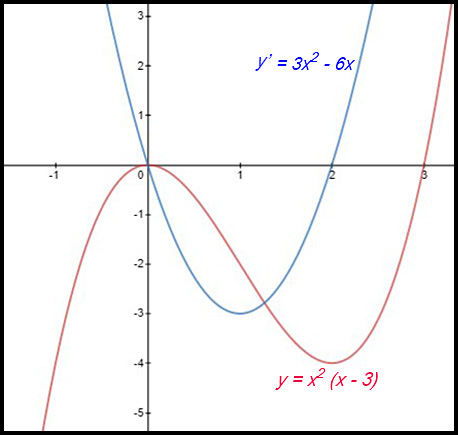
As this is a maximum value (by observation) for the slope
of the original curve, there is a point of inflection at x = 0.833.
  6. y = x2(x - 3)

(iii) When x = 0, the original curve is at a local maximum
(i.e. zero gradient for the tangent) while the value
for the derivative curve is zero.

When x = 2, the original curve is at a local minimum
(i.e. zero gradient for the tangent - in other words the value
for the derivative curve is zero).

When x = 1, the original curve has a value of about -2
(and the gradient is negative as the curve is decreasing ).
The value for the derivative curve is -3 (the value is not really relevant here) but it is a minimum for that curve indicating a point of inflection
for the original curve.
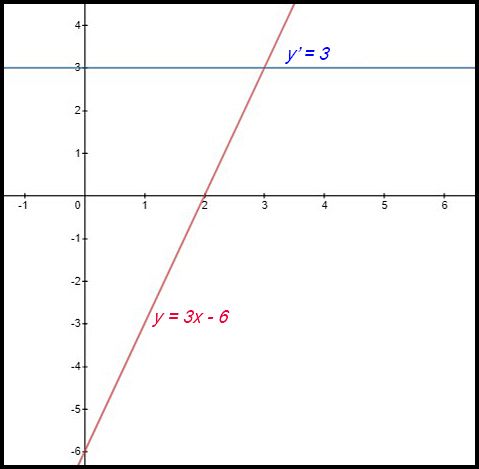
Given a line 7. y = 3x - 6

The graph of the line y = 3x - 6 shows an increasing function
with a constant gradient.

The graph of the derivative y' = 3 shows the constancy
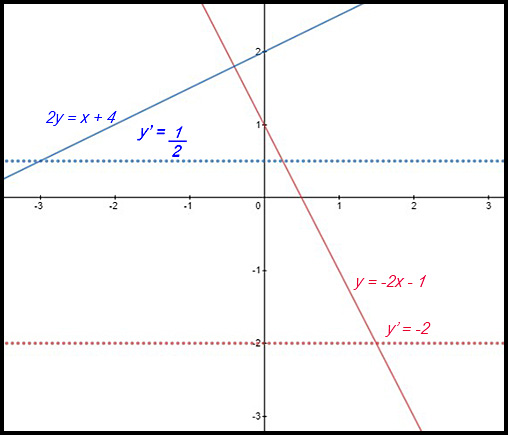
of the gradient as a striaght horizontal line.
 

8. y = -2x + 1 and 2y = x + 4

The two original equations have gradients which are perpendicular and so the graphs (in unbroken lines) meet at right angles.

The two gradient curves (in dotted lines) are horizontal
as for all gradients of linear equations.
The product of their distances from the x-axis equals -1
(not that we can see that easily).
  9. y = -5.

The original function y = -5 is a straight horizontal line.
It therefore has a gradient of 0.

Hence the graph of the gradient function is also a straight horizontal along the x axis (showing the zero gradient).
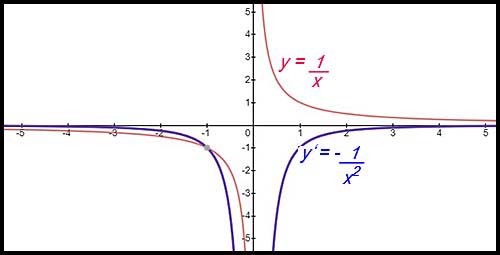
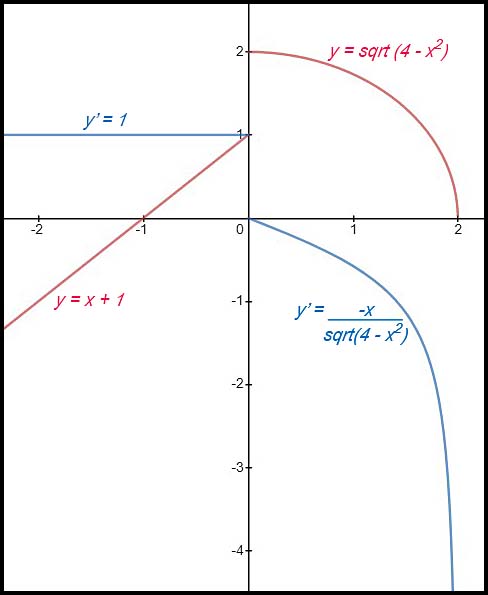
Given a hyperbola. 10.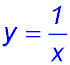

  11.

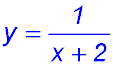
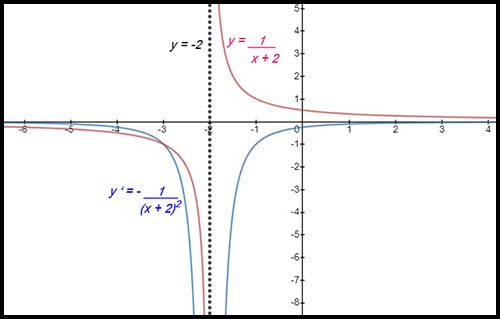
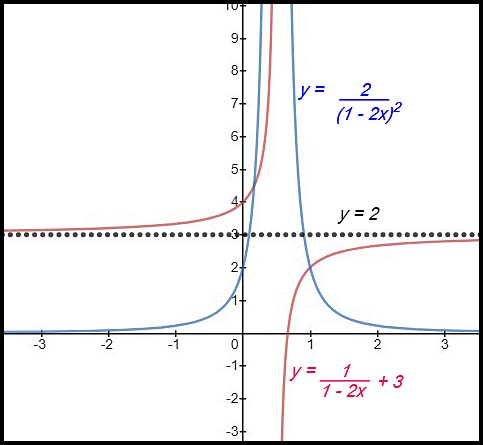
  12.

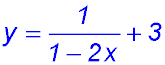
(i) The original hyperbola is shifted up 3 units.

(ii) The constant term for the original function
is a location constant. It merely shift the curve
up (or down) vertically but it does not affect
the gradient of the curve. Hence it plays no part
in the losation of the derivative curve.
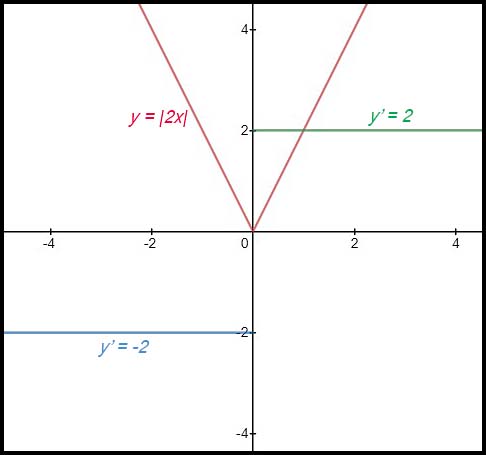
Given an absolute value.

13. f(x) = |2x|.

At x = 0, the gradient is undefined.
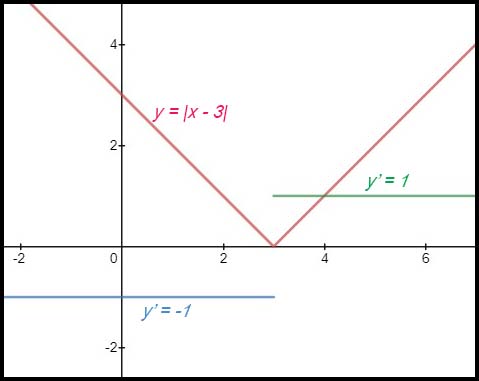
Hence the two lines for the derivative are not defined at x = 0.

 

14. f(x) = |x - 3|

At x = 3, the gradient is undefined.
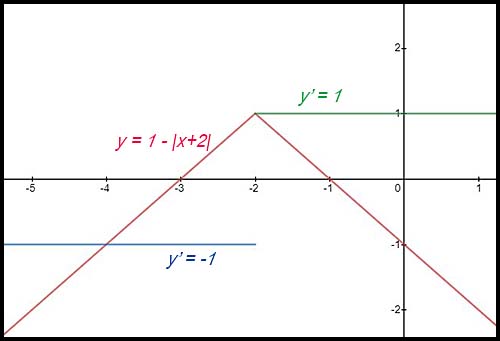
Hence the two lines for the derivative are not defined at x = 3.

 

15. y = 1 - |x + 2|
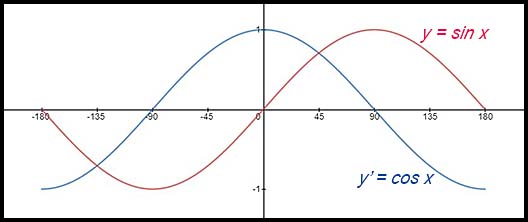
Given a trig function.

16. y = sin x for x: [-180°, 180°].
 

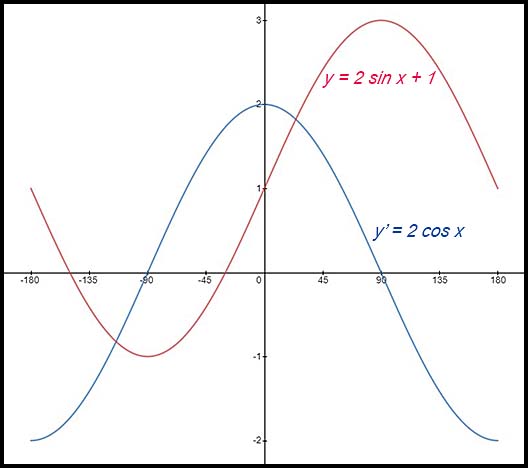
17. y = 2sin x + 1 for x: [-180°, 180°].
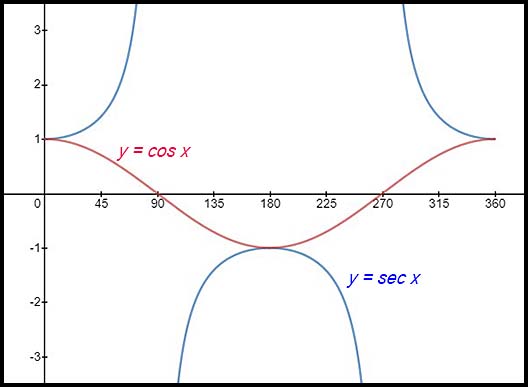
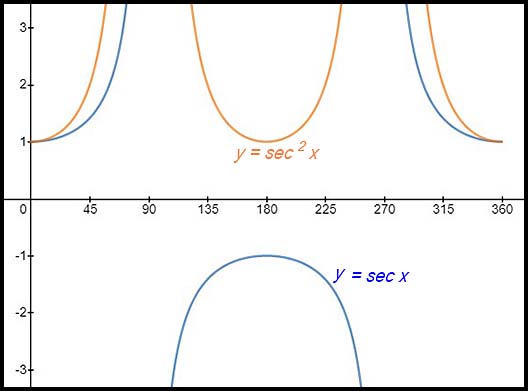
  18. (i) Draw y = cos x for x: [0°, 360°].

(ii) Using your graph, draw the graph of y = sec x.

Note: at x = 90° and x = 270°, forming y = sec x requires a division by zero and so the function is undefined.

At x = 0° and 360°, there is a division by 1 and
at x = 180°, the division is by -1 -
so the curve below the axis becomes inverted .

(iii) Hence draw the derivative graph of y = sec2 x.
Mixed functions (piecewise). 19. y = -2 - x with x: (- ∞, -2]

y = 4 - x2 with x: (-2, 2)

y = x - 2 with x: [2, ∞)

  20. y = x + 1 for x: (-∞ , 0]

for x: (0, 2]
  21.

From given graphs.
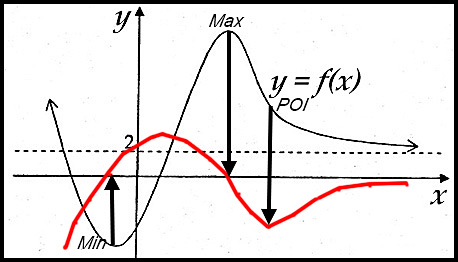
Given a graph 22. The graph of y = f(x) is shown below with its derivative curve.

To draw the derivative curve, follow the steps previously outlined:

1. draw arrows from the stationary points to the x axis
and mark those points (shown in black above but draw lightly so you can erase).

2. examine the gradient of the original curve on either side
of the stationary points starting from the left point.
If a positive gradient, draw a curve above the x axis
down to the point.
If negative, draw a curve below the x axis up to the point.

3. Continue this process for each stationary point.

 
  23.

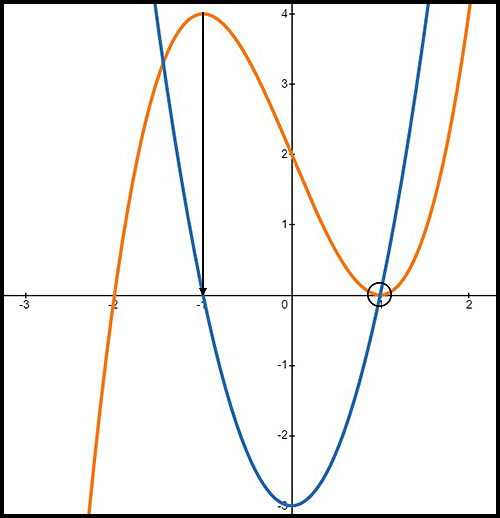
Note: By inspection, the original curve is y = (x + 2)(x - 1)2.

As with the previous sketch:

1. draw arrows from the stationary point at x = 2 to the x axis and mark that point then also mark the stationary point at x = 1 on the x axis.

2. To the left of x = -2, the gradient is positive so draw a curve above the axis down to that point.

3. To the right of x = -2, the gradient is negative so draw a curve below the axis moving away from that point.

4. Repeat that approach for the curve around x = 1.

5. Between these two points on the x axis representing the stationary points, there is a point of inflection at x = 0. Link your two lines on the gradient graph to meet as a minimum point on the y axis.

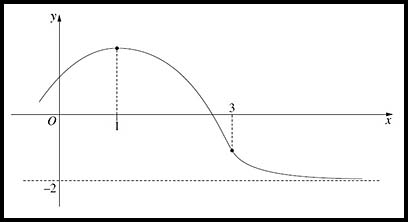
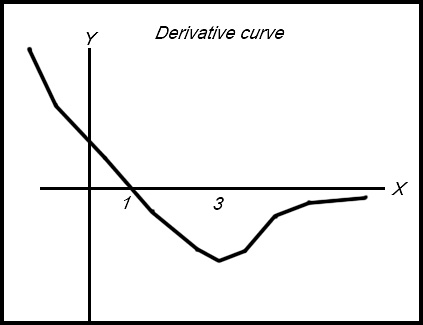
  24. The diagram shows a function having:
  • a stationary point at x = 1;
  • a point of inflection at x = 3; and
  • a horizontal asymptote at y = -2.

Try to finish with a smooth graph.
  25.
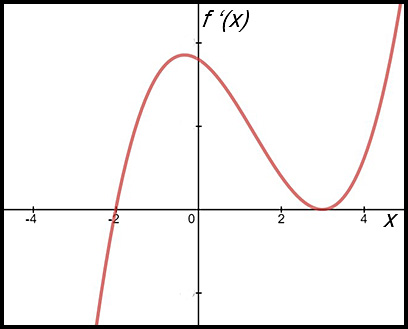
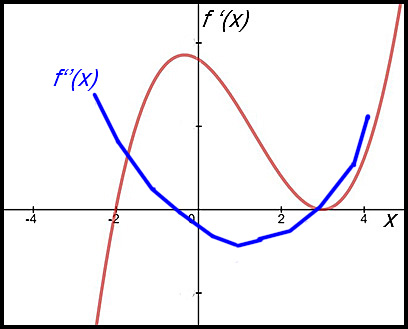
Drawing a second derivative curve. 26. The following diagram shows the graph of a derivative function f '(x) for the domain [-2.5, 4]. Assume f (0) = 0.


Make your graph as smooth as you can.
 

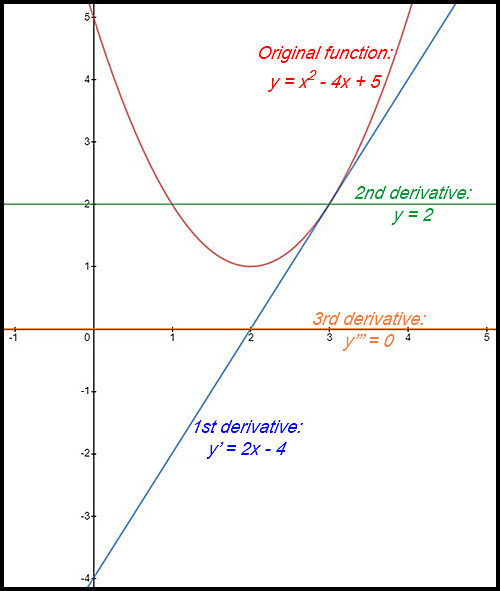
27. (i) For the function

y = x2 - 4x + 5.

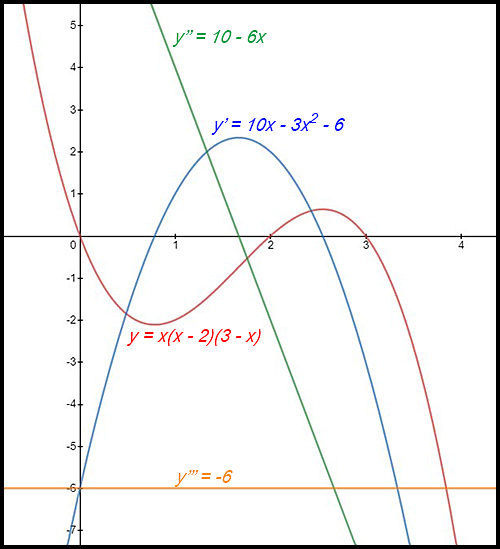
the first three derivatives of the function are shown below:
 

28. For the function y = x(x - 2)(3 - x):